Question

Bicycles 14mph with no wind. Against the wind, bikes 10 mi in

the same time it takes to bike 20 mi with the wind. What is the speed of
the wind?​

Answer 1

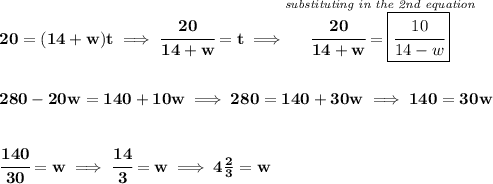
recall your d = rt, distance = rate * time.

w = speed of the wind.

14 = speed of the bicycle without wind.

now, against the wind, the bicycle is not really going 14 mph fast, is really going "14 - w", since the wind is eroding speed from it, likewise, when the bicycle is going with the wind is not going 14 mph fast either, is really going "14 + w" due to the wind adding speed, let's say it took "t" hours against and also "t" hours with it.

`\bf \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ \textit{against the wind}&10&14-w&t\\ \textit{with the wind}&20&14+w&t \end{array}~\hfill \begin{cases} 10=(14-w)t\\ (10)/(14-w)=\boxed{t}\\ \cline{1-1} 20=(14+w)t \end{cases}`

`\bf 20=(14+w)t\implies \cfrac{20}{14+w}=t\implies \stackrel{\textit{substituting in the 2nd equation}}{\cfrac{20}{14+w}=\boxed{\cfrac{10}{14-w}}} \\\\\\ 280-20w=140+10w\implies 280=140+30w\implies 140=30w \\\\\\ \cfrac{140}{30}=w\implies \cfrac{14}{3}=w\implies 4(2)/(3)=w`