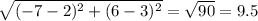Answer:
(7, 3), (–1, –1) and (2, 8) are at a distance of units from (2, 3).
Explanation:
We know that the formula of distance is given by:
Distance =
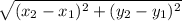
So substituting the given points points to check which points are at a distance of 5 units from
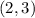 .
.
1. (2, 3) and (7, 3):

2. (2, 3) and (–1, –1):
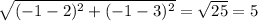
3. (2, 3) and (0, 3):
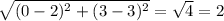
4. (2, 3) and (2, 8):
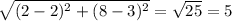
5. (2, 3) and (-7, 6):