Question

Determine the concavity of the curve with parametric equations x = t2, y = t3 - 3t at t = 2. justify your answer.

Answer 1

Use the chain rule to find the first and second derivatives of
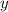`y` with respect to
`x`.

`(dy)/(dx) = (dy)/(dt)\cdot(dt)/(dx) = (dy/dt)/(dx/dt)`

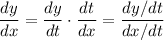
Differentiate the parametric equations with respect to
`t`.

`x(t) = t^2 \implies (dx)/(dt) = 2t`

`y(t) = t^3 - 3t \implies (dy)/(dt) = 3t^2 - 3`

`\implies (dy)/(dx) = (3t^2 - 3)/(2t)`

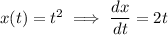
Let
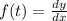`f(t) = (dy)/(dx)`. By the chain rule,

`(d^2y)/(dx^2) = (df)/(dx) = (df)/(dt) \cdot (dt)/(dx) = \frac[df/dt}{dx/dt}`

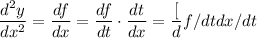
Differentiate
`f`.

`f(t) = (3t^2 - 3)/(2t) = \frac32t - \frac3{2t} \implies (df)/(dt) = (d^2y)/(dx^2) = \frac32 + \frac3{2t^2}`

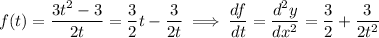
At
`t=2`, the second derivative has a positive sign, so the curve is concave upward at this point.