Answer:
she can make 50 different selections!
Explanation:
To find the different selections that can be made, we use the formula:
nCr = n! / r! * (n - r)!. Where 'n' represents the number of items available and 'r' represents the nuber of items being chosen
In this case:
'n' equals 10 and 'r' equals 2. Therefore:
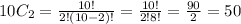
So she can make 50 different selections!