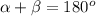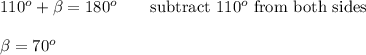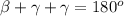Answer:
x = 70°
y = 55°
z = 55°
Explanation:
Look at the picture.
We know: the sum of the angles measure in the triangle is 180°. Therefore we have the equation:
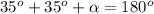
Solve it:
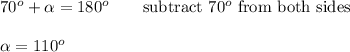
Angle α and β = x are the supplementary angles. Supplementary angles add up to 180°. Therefore: