Question

Given that the first term and the common difference of an arithmetic progression are 6 and 3 respectively. Calculate the sum of all terms from 4th term to the 14th term.​

Answer 1

330

Explanation:

Evaluate the sum of 14 terms and subtract the sum of the first 3 terms

The sum to n terms of an arithmetic sequence is

`S_(n)` =
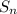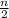`(n)/(2)` [ 2a₁ + (n - 1)d ], so

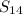`S_(14)` = 7 [ (2 × 6) + (13 × 3)]

= 7(12 + 39) = 7 × 51 = 357

`S_(3)` = 6 + 9 + 12 = 27

Sum of terms from 4 th to 14 th = 357 - 27 = 330