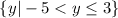Question

Finding the Domain and Range of a Graph

Determine the domain and range for the graph below. Write your answer in interval notation and in set builder form using a compound inequality.

Domain written in interval notation:

Range written in interval notation:

Domain written in set builder form
Use a compound inequality:

x


Range written in set builder form
Use a compound inequality:

y

Answer 1

Explanation:

By looking at the graph I notice an open circle at (-4, -5) which means the function is not evaluable at -4, this restricts the domain.

The Domain of a function represents the set of values for which the function has an output.

The Range of a function is the set containing all the possible values associated with all input.

Domain in interval notation: (-4, 3]. The parenthesis denotes that the interval does not contain the extreme point -4. The brackets are the opposite.

Domain in set builder notation:
`$\-4<x \leq 3 \$`

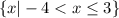
Range in interval notation: (-5, -3]

Range in set builder notation:
`$\y $`

Answer 2

1) Domain = -4 < x ≤ 3

Explanation:

In this case, we have a line segment made up by two points (-4,-5) and (3,-3)

1) To find the Domain, is to find the set of values x may assume for a function.

We can also write it as compound inequality which is a complete form of writing it since inform us the set, the conditions.

x ∈ R

Or simply the interval (-4,3]

2) Range or Image is the set of values y may assume once you plug it in valid values for the Domain.

-5>y≥-3 or Simply (-5, -3]