Answer:
The standard form of the equation is 49t² - 75t + 3 = 0
The solution of the equations are 1.49 and 0.041
Explanation:
* Lets explain how to solve the problem
- The standard form of the quadratic equation is ax² + bx + c = 0,
where a , b , c are constant and a can not be 0
∵ The quadratic equation is -4.9t² + 7.5t + 1.8 = 2.1
- Lets make the left hand side equal to 0
∵ -4.9t² + 7.5t + 1.8 = 2.1 ⇒ subtract 2.1 from both sides
∴ -4.9t² + 7.5t - 0.3 = 0 ⇒ multiply each term by -10
∴ 49t² - 75t + 3 = 0
* The standard form of the equation is 49t² - 75t + 3 = 0
∵ ax² + bx + c = 0
∴ a = 49 , b = -75 , c = 3
- Lets use the formula
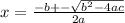 to solve
to solve
the equation
∴
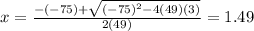
∴
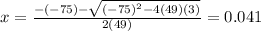
* The solution of the equations are 1.49 and 0.041