Answer:
the number of $10 bills = 17
the number of $20 bills = 37
Explanation:
Let x be the number of $10 bills and y be the number of $20 bills
Total bills = 54
So
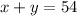
Total value of money is $910
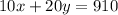
now we solve for x and y
Solve the first equation for y
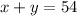
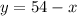
Now replace y in second equation
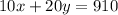
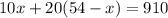

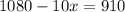
Subtract 1080 from both sides
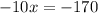
Divide both sides by -10
x= 17
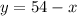
Replace x with 17
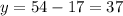
the number of $10 bills = 17
the number of $20 bills = 37