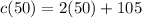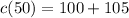Answer:
a.

b.

Explanation:
The variable cost of $ 2 implies that for each manufactured calculator the total cost increases $ 2.
The fixed cost of $ 105 implies that regardless of the number of manufactured calculators there will always be a cost of $ 105.
If we call x the number of manufactured calculators then the total cost c(x) will be:

Then, the cost of manufactured 50 calculators a day is: