Question

Cos^2a/(1-tana)+sin^3a/(sina-cosa)=sina+cosa
​

Answer 1

`\large\boxed{a=2k\pi\ for\ k\in\mathbb{Z}}`

Explanation:

`\bold{a=x}`

`\text{The domain:}\\\\1-\tan x\\eq0\ \wedge\ \sin x-\cos x\\eq0\ \wedge\ x\\eq(\pi)/(2)+k\pi\ (from\ \tan x)\\\\\tan x\\eq1\ \wedge\ \sin x\\eq\cos x\\\\x\\eq(\pi)/(4)+k\pi\ \wedge\ x\\eq(\pi)/(4)+k\pi\ for\ k\in\mathbb{Z}`

`(\cos^2x)/(1-\tan x)+(\sin^3x)/(\sin x-\cos x)=\sin x+\cos x`

`\text{Left side of the equation:}`

`\text{use}\ \tan x=(\sin x)/(\cos x)\\\\(\cos^2x)/(1-\tan x)=(\cos^2x)/(1-(\sin x)/(\cos x))=(\cos^2x)/((\cos x)/(\cos x)-(\sin x)/(\cos x))=(\cos^2x)/((\cos x-\sin x)/(\cos x))=\cos^2x\cdot(\cos x)/(\cos x-\sin x)\\\\=(\cos^3x)/(\cos x-\sin x)\\\\(\cos^2x)/(1-\tan x)+(\sin^3x)/(\sin x-\cos x)=(\cos^3x)/(\cos x-\sin x)+(\sin^3x)/(\sin x-\cos x)\\\\=(\cos^3x)/(\cos x-\sin x)+(\sin^3x)/(-(\cos x-\sin x))`

`=(\cos^3x)/(\cos x-\sin x)-(\sin^3x)/(\cos x-\sin x)\\\\=(\cos^3x-\sin^3x)/(\cos x-\sin x)\qquad\text{use}\ a^3-b^3=(a-b)(a^2+ab+b^2)\\\\=((\cos x-\sin x)(\cos^2x+\cos x\sin x+\sin^2x))/(\cos x-\sin x)\qquad\text{cancel}\ (\cos x-\sin x)\\\\=\cos^2x+\cos x\sin x+\sin^2x\qquad\text{use}\ \sin^2x+\cos^2x=1\\\\=\cos x\sin x+1`

`\text{We're back to the equation}`

`\cos x\sin x+1=\sin x+\cos x\qquad\text{subtract}\ \sin x\ \text{and}\ \cos x\ \text{from both sides}\\\\\cos x\sin x+1-\sin x-\cos x=0\\\\(\cos x\sin x-\sin x)+(1-\cos x)=0\\\\\sin x(\cos x-1)-1(\cos x-1)=0\\\\(\cos x-1)(\sin x-1)=0\iff \cos x-1=0\ or\ \sin x-1=0\\\\\cos x=1\ or\ \sin x=1\\\\x=2k\pi\in D\ or\ x=(\pi)/(2)+2k\pi\\otin D\ for\ k\in\mathbb{Z}`

Answer 2

a=2*n*pi where n is an integer

Explanation:

`(\cos^2(a))/(1-\tan(a))+(\sin^3(a))/(\sin(a)-\cos(a))`

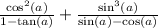
The denominators are different here so I'm going to try to make them the same.

I'm going to write everything in terms of sine and cosine.

That means I'm rewriting tan(a) as sin(a)/cos(a)

`(\cos^2(a))/(1-(\sin(a))/(\cos(a)))+(\sin^3(a))/(\sin(a)-\cos(a))`

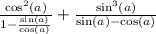
I'm going to multiply top and bottom of the first fraction by cos(a) to clear the mini-fraction from the bigger fraction.

`(\cos^2(a))/(1-(\sin(a))/(\cos(a))) \cdot \frac{\cos(a)}}{\cos(a)}+(\sin^3(a))/(\sin(a)-\cos(a))`

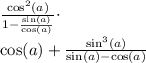
Distributing and Simplifying:

`(\cos^3(a))/(\cos(a)-\sin(a))+(\sin^3(a))/(\sin(a)-\cos(a))`

Now I see the bottom's aren't quite the same but they are almost... They are actually just the opposite. That is -(cos(a)-sin(a))=-cos(a)+sin(a)=sin(a)-cos(a).

Or -(sin(a)-cos(a))=-sin(a)+cos(a)=cos(a)-sin(a).

So to get the denominators to be the same I'm going to multiply either fraction by -1/-1... I'm going to do this to the second fraction.

`(\cos^3(a))/(\cos(a)-\sin(a))+(\sin^3(a))/(\sin(a)-\cos(a)) \cdot (-1)/(-1)`

`(\cos^3(a))/(\cos(a)-\sin(a))+(-\sin^3(a))/(\cos(a)-\sin(a))`

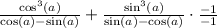
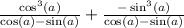
The bottoms( the denominators) are the same now. We can write this as one fraction, now.

`(\cos^3(a)-\sin^3(a))/(\cos(a)-\sin(a))`

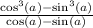
I don't know if you know but we can factor a difference of cubes.

The numerator is in the form of a^3-b^3.

The formula for factoring that is (a-b)(a^2+ab+b^2).

`((\cos(a)-\sin(a))(\cos^2(a)+\cos(a)\sin(a)+\sin^2(a))/(\cos(a)-\sin(a))`

There is a common factor of cos(a)-sin(a) on top and bottom you can "cancel it".

So we now have

`\cos^2(a)+\cos(a)\sin(a)+\sin^2(a)`

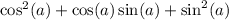
We can actually simplify this even more.

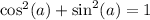`\cos^2(a)+\sin^2(a)=1` is a Pythagorean Identity.

So we rewrite
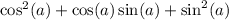
`\cos^2(a)+\cos(a)\sin(a)+\sin^2(a)`

as
`1+\cos(a)\sin(a)`

So that is what we get after simplifying left hand side.

So I guess we are trying to solve for a.

`1+\cos(a)\sin(a)=\sin(a)+\cos(a)`

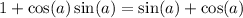
Subtract sin(a) and cos(a) on both sides.

`\cos(a)\sin(a)-\sin(a)-\cos(a)+1=0`

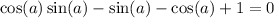
This can be factored as

`(\sin(a)-1)(\cos(a)-1)=0`

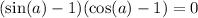
So we just need to solve the following two equations:

`\sin(a)-1=0 \text{ and } \cos(a)-1=0`

`\sin(a)=1 \text{ and } cos(a)=1 \text{ I just added one on both sides}`

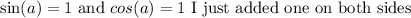
Now we just need to think of the y-coordinates on the unit circle that are 1

and the x-coordinates being 1 also (not at the same time of course).

List thinking of the y-coordinates being 1:

a=pi/2 , 5pi/2 , 9pi/2 , ....

List thinking of the x-coordinates being 1:

a=0, 2pi, 4pi,...

So let's come up with a pattern for these because there are infinite number of solutions that continue in this way.

If you notice in the first list the number next to pi is going up by 4 each time.

So for the first list we can say a=(4pi*n+pi)/2 where n is an integer.

The next list the number in front of pi is just even.

So for the second list we can say a=2*n*pi where n is an integer.

So the solutions is a=2*n*pi , a=(4pi*n+pi)/2

We really should make sure if this is okay for our original equation.

We don't have to worry about the second fraction because sin(a)=cos(a) only when a is pi/4 or pi/4+2pi*n OR (pi+pi/4) or (pi+pi/4)+2pi*n.

Now the second fraction we have 1-tan(a) in the denominator, and it is 0 when:

tan(a)=1

sin(a)/cos(a)=1 => sin(a)=cos(a)

So the only thing we have to worry about here since we said sin(a)=cos(a) doesn't hurt our solution is the division by the cos(a).

When is cos(a)=0?

cos(a)=0 when a=pi/2 or any rotations that stop there (+2npi thing) or at 3pi/2 (+2npi)

So the only solutions that work is the a=2*n*pi where n is an integer.