Answer: OPTION C.
Explanation:
In order to find the average rate of change for this function for the given quadratic function, for the interval from
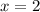 to
to
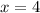 , you can use this formula:
, you can use this formula:
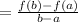
In this case, you can identify that:
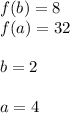
Then, substituting values into the formula, you get this result:
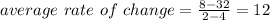
This matches with the option C.