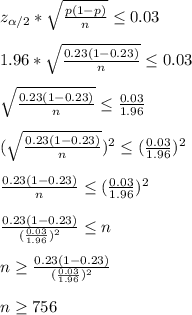Question

The state education commission wants to estimate the fraction of tenth grade students that have reading skills at or below the eighth grade level. in an earlier study, the population proportion was estimated to be 0.23. how large a sample would be required in order to estimate the fraction of tenth graders reading at or below the eighth grade level at the 95% confidence level with an error of at most 0.03? round your answer up to the next integer.

Answer 1

1305

Explanation:

Answer 2

The sample size must be greater than or equal to 756

Explanation:

The formula to calculate the error of the proportion is the following

`E=z_(\alpha/2)*\sqrt{(p(1-p))/(n)}`

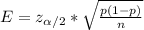
where p is the proportion, n the sample size, E is the error and z is the z-score for a confidence level of 95%

For a confidence level of 95%
`z_(\alpha/2)=1.96`

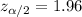
We know that for this case
`p=0.23`

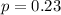
We require that the error be 0.03 as maximum

Therefore we solve for the variable n

`z_(\alpha/2)*\sqrt{(p(1-p))/(n)}\leq0.03\\\\1.96*\sqrt{(0.23(1-0.23))/(n)}\leq0.03\\\\\sqrt{(0.23(1-0.23))/(n)}\leq (0.03)/(1.96)\\\\(\sqrt{(0.23(1-0.23))/(n)})^2\leq ((0.03)/(1.96))^2\\\\(0.23(1-0.23))/(n)\leq ((0.03)/(1.96))^2\\\\(0.23(1-0.23))/(((0.03)/(1.96))^2)\leq n\\\\n\geq(0.23(1-0.23))/(((0.03)/(1.96))^2)\\\\n\geq756`