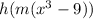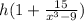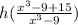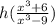Write the function , √(x^3+6)/√(x^3-9) as a composition of three or more non-identity functions.

Question

asked May 1, 2020 65.4k views

1 Answer

Jimbeeer · Answer 1 · 2020-05-05T16:39:14+0000

Answer:

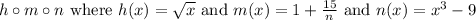
$h \circ m \circ n \text{ where } h(x)=√(x) \text{ and } m(x)=1+(15)/(n) \text{ and } n(x)=x^3-9$

Explanation:

Ok so I see a square root is on the whole thing.

I'm going to let the very outside function by
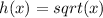h(x)=sqrt(x) .

Now I'm can't just let the inside function by one function
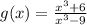g(x)=(x^3+6)/(x^3-9) because we need three functions.

So I'm going to play with
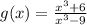g(x)=(x^3+6)/(x^3-9) a little to simplify it.

You could do long division. I'm just going to rewrite the top as

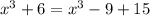x^3+6=x^3-9+15 .

g(x)=(x^3-9+15)/(x^3-9)=1+(15)/(x^3-9) .

So I'm going to let the next inside function after h be
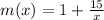m(x)=1 + (15)/(x) .

Now my last function will be
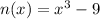n(x)=x^3-9 .

So my order is h(m(n(x))).

Let's check it:

h(m(x^3-9))

h(1+(15)/(x^3-9))

h((x^3-9+15)/(x^3-9))

h((x^3+6)/(x^3-9))

$\sqrt{ (x^3+6)/(x^3-9)}$