Answer: 0.4302
Explanation:
Given : Mean :
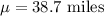
Standard deviation :
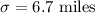
Sample size :

Also, these distances are normally distributed.
Then , the formula to calculate the z-score is given by :-

For x=32.5
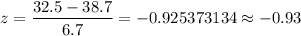
For x=40.5
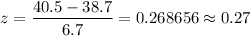
The p-value =
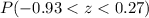
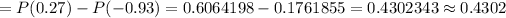
Hence, the required probability :-0.4302