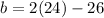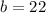Question

The shortest side of an isosceles triangle is 26 cm less than twice as long as the other sides. The perimeter of the triangle is 70 cm. Find the lengths of the three sides and list them in ascending order.

___cm, ____cm, ____cm

Answer 1

22cm,24cm,24cm

Explanation:

Let us call one of the other sides x

the shortest side = 2x-26

in an isosceles, 2 sides are equal (x in this case)

so we now have sides of x,x and 2x-26

form an eqution from this.

4x-26=70

4x=96

x=24

24 x 2 = 48 - 26 = 22

thus, the shortest side is 22cm and the other sides are both 24cm

Answer 2

The lengths of the three sides in ascending order is.

_22__cm, __24__cm, __24__cm

Explanation:

The perimeter of a triangle is equal to the sum of the length of its three sides.

By definition, an isosceles triangle has two equal sides.

We know that the short side measures 26 cm less than twice as long as the other sides, and that the other two sides are of equal length.

We also know that the perimeter of the triangle is 70 cm

Then we propose the following equation

`P = b + 2s`

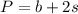
Where P is the perimeter, b is the shortest side of the triangle and s is the length of the equal sides.

Then:

`b= 2s -26`

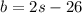
We substitute this equation in the first equation and solve for s

`P = 2s -26 + 2s`

`P = 4s -26=70`

`4s -26=70`

`4s=70 +26`

`4s=96`

`s=(96)/(4)`

`s=24`

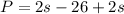
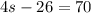
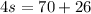
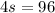
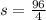
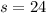
Then

`b= 2(24) -26`

`b= 22`