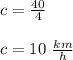Answer:
1)
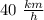
2)
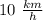
Explanation:
Let' call "b" the speed of the motorboat and "c" the speed of the current.
We know that:

Where "V" is the speed, "d" is distance and "t" is time.
Then:
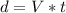
We know that distance traveled upstream is 150 km and the time is 5 hours. Then, we set up the folllowing equation:
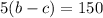 (Remember that in the trip upstream the speed of the river is opposite to the motorboat)
(Remember that in the trip upstream the speed of the river is opposite to the motorboat)
For the return trip:
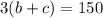
By solving the system of equations, we get:
- Make both equations equal to each other and solve for "c".

- Substitute "c" into the any original equation and solve for "b":

- Substitute "b" into
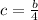 :
: