Question

A factory tests 100 light bulbs for defects. The probability that a bulb is defective is 0.02. The occurrences of defects among the light bulbs are mutually independent events. Calculate the probability that exactly two are defective given that the number of defective bulbs is two or fewer.

Answer 1

The probability that exactly two are defective given that the number of defective bulbs is two or fewer is 0.4040.

Explanation:

Let X be the number of defective bulbs.

`X\sim B(n,p)`

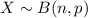
Where n is sample size and p is probability of success.

According to the given information,

`n=100`

`p=0.02`

`q=1-p=1-0.02=0.98`

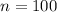
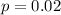
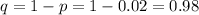
According to binomial distribution the probability of exactly r success from n is

`P(X=r)=^nC_rp^rq^(n-r)`

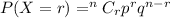
The probability that exactly two are defective is

`P(X=2)=^(100)C_2(0.02)^2(0.98)^(98)\approx 0.2724`

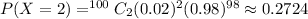
The probability that the number of defective bulbs is two or fewer is

`P(X\leq 2)=P(X=0)+P(X=1)+P(X=2)`

`P(X\leq 2)=^(100)C_0(0.02)^0(0.98)^(100)+^(100)C_1(0.02)^1(0.98)^(99)+^(100)C_2(0.02)^2(0.98)^(98)`

`P(X\leq 2)=0.1326+0.2707+0.2734`

`P(X\leq 2)=0.6767`

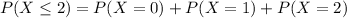
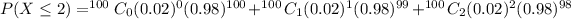
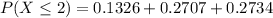
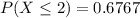
We have to find the probability that exactly two are defective given that the number of defective bulbs is two or fewer.

`P(x=2|x\leq 2)`

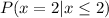
According to the conditional probability

`P((A)/(B))=(P(A\cap B))/(P(B))`

`P(x=2|x\leq 2)=(P(x=2\cap x\leq 2))/(P(x\leq 2))`

`P(x=2|x\leq 2)=(P(x=2))/(P(x\leq 2))`

`P(x=2|x\leq 2)=(0.2734)/(0.6767)=0.4040`

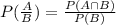
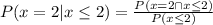
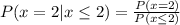
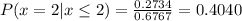
Therefore the probability that exactly two are defective given that the number of defective bulbs is two or fewer is 0.4040.