Question

Suppose your credit card issuer states that it charges a 15.00% nominal annual rate, but you must make weekly payments, which amounts to weekly compounding. what is the effective annual rate? 15.27% 16.08% 16.16% 16.56% 18.61%

Answer 1

16.16%

Step-by-step explanation:

Given that:

A credit card issuer states that it charges a 15.00% nominal annual rate = 0.15

And which you must make weekly payments i.e weekly compounding, Therefore, there are 52 periods in a year.

The Effective annual rate (EAR) can be calculated by the formula;

`(EAR) = (1+(annual rate)/(number of periods))^(number of periods) -1`

=
`(1+(0.15)/(12))^(52) -1`

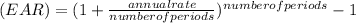
∴ we have;

= (1 + 0.002885)⁵² - 1

= (1.002885)⁵² - 1

= 1.16160656 - 1

= 0.16160656

= 16.160656 %

≅ 16.16 %

∴ The effective annual rate (EAR) = 16.16%

Answer 2

16.16%

Step-by-step explanation:

The multiplier each week is ...

1 + 15%/52

So the multiplier after 52 weeks is ...

(1 +.15/52)^52 ≈ 1.1615834

This corresponds to an effective annual interest rate of 16.16%.