Question

A specimen of copper having a rectangular cross section 15.2 mm X19.1 mm (0.6 in. X 0.75 in.) is pulled in tension with 44500 N(10000 lbf) force, producing only elastic deformation. Calculate the resulting strain.

Answer 1

The elastic deformation is 0.00131.

Step-by-step explanation:

Given that,

Force F = 44500 N

Cross section
`A =15.2mm*19.1\ mm`

We Calculate the stress

Using formula of stress

`\sigma=(F)/(A)`

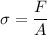
Where, F = force

A = area of cross section

Put the value into the formula

`\sigma=(44500)/(15.2*10^(-3)*19.1*10^(-3))`

`\sigma=153.27*10^(6)\ N/m^2`

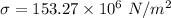
We need to calculate the strain

Using formula of strain

`Y=(\sigma)/(\epsilon)`

`epsilon=(\sigma)/(Y)`

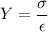
Where,

`\sigma`=stress

Y = young modulus of copper

Put the value into the formula

`\epsilon=(153.27*10^(6))/(117*10^(9))`

`\epsilon =0.00131`

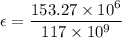
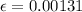
Hence, The elastic deformation is 0.00131.