Answer:

Explanation:
Answer:
Explanation:
Given : A random sample of 10 subjects have weights with a standard deviation of 11.9407 kg
i.e.
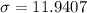
Since we know that the value of variance is the square of standard deviation.
i.e.

Therefore, to find the value of variance, we need to find the square of the given standard deviation.
i.e.
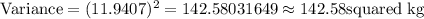
Thus, the variance of their weights =
