Question

A rancher has 800 feet of fencing to put around a rectangular field and then subdivide the field into 2 identical smaller rectangular plots by placing a fence parallel to one of the field's shorter sides. Find the dimensions that maximize the enclosed area. Write your answers as fractions reduced to lowest terms.

Answer 1

The dimensions of enclosed area are 200 and 400/3 feet

Explanation:

* Lets explain how to solve the problem

- There are 800 feet of fencing

- We will but it around a rectangular field

- We will divided the field into 2 identical smaller rectangular plots

by placing a fence parallel to one of the field's shorter sides

- Assume that the long side of the rectangular field is a and the

shorter side is b

∵ The length of the fence is the perimeter of the field

∵ We will fence 2 longer sides and 3 shorter sides

∴ 2a + 3b = 800

- Lets find b in terms of a

∵ 2a + 3b = 800 ⇒ subtract 2a from both sides

∴ 3b = 800 - 2a ⇒ divide both sides by 3

∴
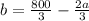`b=(800)/(3)-(2a)/(3)` ⇒ (1)

- Lets find the area of the field

∵ The area of the rectangle = length × width

∴ A = a × b

∴
`A=(a).((800)/(3)-(2a)/(3))=(800a)/(3)-(2a^(2))/(3)`

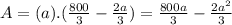
- To find the dimensions of maximum area differentiate the area with

respect to a and equate it by 0

∴
`(dA)/(da)=(800)/(3)-(4a)/(3)`

∵
`(dA)/(da)=0`

∴
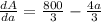
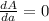
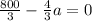`(800)/(3)-(4)/(3)a=0` ⇒ Add 4/3 a to both sides

∴
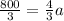`(800)/(3)=(4)/(3)a` ⇒ multiply both sides by 3

∴ 800 = 4a ⇒ divide both sides by 4

∴ 200 = a

- Substitute the value of a in equation (1)

∴
`b=(800)/(3)-(2)/(3)(200)=(800)/(3)-(400)/(3)=(400)/(3)`

* The dimensions of enclosed area are 200 and 400/3 feet