Answer:
The answer in the procedure
Explanation:
we know that
The volume of a rectangular pyramid is equal to
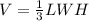
where
L is the length of the rectangular base
W is the width of the rectangular base
H is the height of the pyramid
If the pyramid is scaled proportionally by a factor of k
then
the new dimensions are
L=kL
W=kW
H=kH
substitute and find the new Volume V'
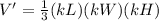
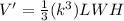
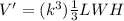
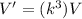
The new volume is equal to the scale factor k elevated to the cube multiplied by the original volume