Question

Alyssa is jogging near Central Park. She runs along 65th Street for about 0.19 miles, then turns right and runs along Central Park West for about 0.28 miles. She then turns right again and runs along Broadway until she reaches her starting point. How long is her total run to the nearest hundredth of a mile?

Answer 1

about 0.81 miles

Explanation:

Alyssa's route can be considered a right triangle with legs of length 19 and 28 (hundredths). The Pythagorean theorem tells us the hypotenuse (x) will satisfy ...

x^2 = 19^2 +28^2

x^2 = 1145

x = √1145 ≈ 34 . . . . hundredths of a mile

Then Alyssa's total route is ...

0.19 + 0.28 + 0.34 = 0.81 . . . . miles

Answer 2

Her total run is 0.81 miles.

Explanation:

Consider the provided information.

The provided information can be visualized by the figure 1.

The path she covers represent a right angle triangle, where the length of two legs are given as 0.19 and 0.28.

Use the Pythagorean theorem to find the length of missing side.

`a^2+b^2=c^2`

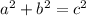
Where, a and b are the legs and c is the hypotenuse of the right angle triangle.

The provided lengths are 0.19 and 0.28.

Now, calculate the missing side.

`(0.19)^2+(0.28)^2=(c)^2`

`0.0361+0.784=(c)^2`

`0.1145=c^2`

`√(0.1145)=c`

`c\approx{0.34}`

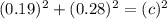
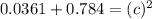
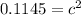
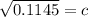
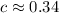
Thus, the total distance is:

0.34 + 0.19 + 0.28 = 0.81

Therefore, her total run is 0.81 miles.