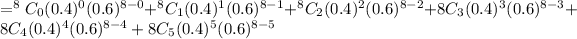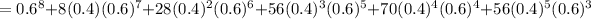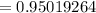Question

Forty percent of households say they would feel secure if they had $50,000 in savings. you randomly select 8 households and ask them if they would feel secure if they had $50,000 in savings. find the probability that the number that say they would feel secure is (a) exactly five, (b) more than five, and (c) at most five.

Answer 1

Let X be the event of feeling secure after saving $50,000,

Given,

The probability of feeling secure after saving $50,000, p = 40 % = 0.4,

So, the probability of not feeling secure after saving $50,000, q = 1 - p = 0.6,

Since, the binomial distribution formula,

`P(x=r)=^nC_r p^r q^(n-r)`

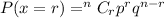
Where,
`^nC_r=(n!)/(r!(n-r)!)`

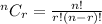
If 8 households choose randomly,

That is, n = 8

(a) the probability of the number that say they would feel secure is exactly 5

`P(X=5)=^8C_5 (0.4)^5 (0.6)^(8-5)`

`=56(0.4)^5 (0.6)^3`

`=0.12386304`

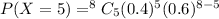
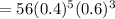
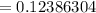
(b) the probability of the number that say they would feel secure is more than five

`P(X>5) = P(X=6)+ P(X=7) + P(X=8)`

`=^8C_6 (0.4)^6 (0.6)^(8-6)+^8C_7 (0.4)^7 (0.6)^(8-7)+^8C_8 (0.4)^8 (0.6)^(8-8)`

`=28(0.4)^6 (0.6)^2 +8(0.4)^7(0.6)+(0.4)^8`

`=0.04980736`

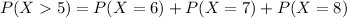
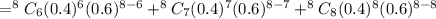
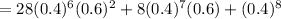
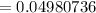
(c) the probability of the number that say they would feel secure is at most five

`P(X\leq 5) = P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)`

`=^8C_0 (0.4)^0(0.6)^(8-0)+^8C_1(0.4)^1(0.6)^(8-1)+^8C_2 (0.4)^2 (0.6)^(8-2)+8C_3 (0.4)^3 (0.6)^(8-3)+8C_4 (0.4)^4 (0.6)^(8-4)+8C_5(0.4)^5 (0.6)^(8-5)`

`=0.6^8+8(0.4)(0.6)^7+28(0.4)^2(0.6)^6+56(0.4)^3(0.6)^5+70(0.4)^4(0.6)^4+56(0.4)^5(0.6)^3`

`=0.95019264`