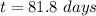Question

MAJORRRR HElppp

Plutonium-210 has a half-life of 140 days. Use the formula , where , is the remaining mass, is the original mass, and is the half-life, to determine how long it takes to reduce 300 milligrams of plutonium-210 to 200 milligrams.
Arrange the steps in the right order to solve the problem.

Answer 1

Step 1: Finding r using the formula ln 2/h

`1.\ r=(ln\ 2)/(h)\\ r=(ln\ 2)/(140)\\r=0.00495`

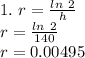
Step 2: Substitute the values in given formula

`2.\ m_t=m_0e^(-rt)\\200=300e^(-0.00495t)`

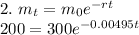
Step 3: Divide both sides by 300

`(2)/(3) =e^(-0.00495t)`

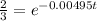
Step 4: Take the natural logarithm on both sides

`ln\ (2)/(3) =ln\ e^(0.00495t)`

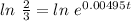
Step 5: Simplify

`-0.405 = -0.00495t`

Step 6: Divide both sides by 0.00495

`(-0.405)/(-0.00495) =t`

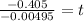
Step 7: Simplify

`t=81.8\ days`