Question

Find an equation for the tangent to the curve at P and the horizontal tangent to the curve at Q. y = 5 + cot x - 2 csc x 0 1 2 3 0 2 4 x y Upper QUpper P left parenthesis StartFraction pi Over 2 EndFraction comma 3 right parenthesis

Answer 1

Answer with explanation:

The given function in x and y is,

y= 5 +cot x-2 Cosec x

To find the equation of tangent, we will differentiate the function with respect to x

`y'= -\csc^2 x+2 \csc x* \cot x`

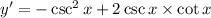
Slope of tangent at (π/2,3)

`y'_{((\pi)/(2),3)}= -\csc^2(\pi)/(2) +2 \csc (\pi)/(2)* \cot (\pi)/(2)\\\\=-1+2* 1 * 0\\\\= -1`

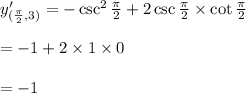
Equation of tangent passing through (π/2,3) can be obtained by

`\rightarrow (y-y_(1))/(x-x_(1))=m(\text{Slope})\\\\ \rightarrow (y-3)/(x-(\pi)/(2))=-1\\\\\rightarrow 3-y=x-(\pi)/(2)\\\\\rightarrow x+y-3-(\pi)/(2)=0`

⇒There will be no Horizontal tangent from the point (π/2,3).