Question

If 1.00 mol of argon is placed in a 0.500-L container at 27.0 degree C , what is the difference between the ideal pressure (as predicted by the ideal gas law) and the real pressure (as predicted by the van der Waals equation)? For argon, a=1.345(L2⋅atm)/mol2 and b=0.03219L/mol. Express your answer to two significant figures and include the appropriate units.

Answer 1

2.0 atm is the difference between the ideal pressure and the real pressure.

Step-by-step explanation:

If 1.00 mole of argon is placed in a 0.500-L container at 27.0 °C

Moles of argon = n = 1.00 mol

Volume of the container,V = 0.500 L

Ideal pressure of the gas = P

Temperature of the gas,T = 27 °C = 300.15 K[/tex]

Using ideal gas equation:

`PV=nRT`

`P=(1.00 mol* 0.0821 L atm/mol K* 300.15 K)/(0.500 L)=49.28 atm`

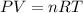
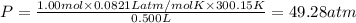
Vander wall's of equation of gases:

The real pressure of the gas=
`p_v`

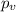
For argon:

`a=1.345 L^2 atm/mol^2`

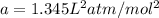
b=0.03219 L/mol.

`(p_v+((an^2)/(V^2))(V-nb)=nRT`

`(p_v+(((1.345 L^2 atm/mol^2)* (1.00 mol)^2)/((0.500 L)^2))(0.500 L-1.00 mol* 0.03219L/mol)=1.00 mol* 0.0821 L atm/mol K* 300.15 K`

`p_v = 47.29 atm`

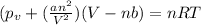
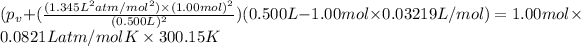
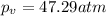
Difference :
`p - p_v= 49.28 atm - 47.29 atm = 1.99 atm\approx 2.0 atm`

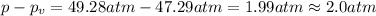
2.0 atm is the difference between the ideal pressure and the real pressure.