Question

Every cereal box has a gift inside, but you cannot tell from the outside what the gift is. The store manager assures you that 11 of the 54 boxes on the shelf have the secret decoder ring. The other 43 boxes on the shelf have a different gift inside. If you randomly select two boxes of cereal from the shelf to purchase, what is the probability that BOTH of them have the secret decoder ring?

Answer 1

The probability that BOTH of them have the secret decoder ring is
`(55)/(1431)`.

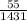Explanation:

From the given information it is clear that the total number of boxes is 54.

Total number of boxes that have the secret decoder ring = 11

Total number of boxes that have a different gift inside = 43

Total number of ways to select 2 boxes from the boxes that have the secret decoder ring is

`\text{Favorable outcomes}=^(11)C_2=(11!)/(2!(11-2)!)=(11* 10* 9!)/(2!9!)=55`

Total number of ways to select 2 boxes from the total number of boxes is

`\text{Total outcomes}=^(54)C_2=(52!)/(2!(52-2)!)=(52* 51* 50!)/(2!50!)=1431`

The probability that BOTH of them have the secret decoder ring is

`P=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`P=(55)/(1431)`

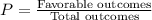
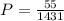
Therefore the probability that BOTH of them have the secret decoder ring is
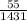`(55)/(1431)`.