Question

Pretend you're playing a carnival game and you've won the lottery, sort of. You have the opportunity to select five bills from a money bag, while blindfolded. The bill values are $1, $2, $5, $10, $20, $50, and $100. How many different possible ways can you choose the five bills? (Order doesn't matter, and there are at least five of each type of bill.) A. 56 B. 120 C. 288 D. 462

Answer 1

Answer: 462

Explanation:

The general theorem of combination says that there are
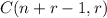`C(n+r-1, r)`, with r-combinations from a set having n elements when repetition of elements is allowed.

Here the number of denomination:
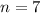`n = 7` , r =5

Also order doesn't matters.

Then the number of different possible ways can you choose the five bills is given by :-
`C(7+5-1, 5)= C(11,5)\\\\=(11!)/(5!(11-5)!)\\\\=462`

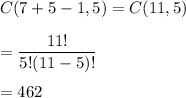
Hence, the number of different possible ways can you choose the five bills is 462.