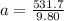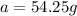Question

A car traveling at 105 km/h strikes a tree. The front end of the car compresses and the driver comes to rest after traveling 0.80 m. (a) What was the magnitude of the average acceleration of the driver during the collision? (b) Express the answer in terms of “g’s,” where 1.00 g = 9.80 m/s^2.

Answer 1

Part a)

a = 531.7 m/s/s

Part b)

a = 54.25 g

Step-by-step explanation:

Part a)

Initial speed of the car is given as

`v = 105 km/h`

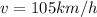
now we have

`v = 29.2 m/s`

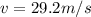
now we know that it stops in 0.80 m

now by kinematics we have

`a = (v_f^2 - v_i^2)/(2d)`

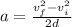
so we will have

`a = (0 - 29.2^2)/(2(0.80))`

`a = 531.7 m/s^2`

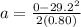
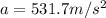
Part b)

in terms of g this is equal to

`a = (531.7)/(9.80)`

`a = 54.25 g`