Answer:
Choice A)
 .
.
Explanation:
What are the changes that would bring
 to
to
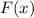 ?
?
- Translate
 to the left by
to the left by
 unit, and
unit, and - Stretch
 vertically (by a factor greater than
vertically (by a factor greater than
 .)
.)
 . The choices of
. The choices of
 listed here are related to
listed here are related to
 :
:
- Choice A)
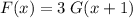 ;
; - Choice B)
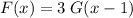 ;
; - Choice C)
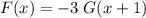 ;
; - Choice D)
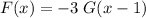 .
.
The expression in the braces (for example
 as in
as in
 ) is the independent variable.
) is the independent variable.
To shift a function on a cartesian plane to the left by
 units, add
units, add
 to its independent variable. Think about how
to its independent variable. Think about how
 , which is to the left of
, which is to the left of
 , will yield the same function value.
, will yield the same function value.
Conversely, to shift a function on a cartesian plane to the right by
 units, subtract
units, subtract
 from its independent variable.
from its independent variable.
For example,
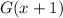 is
is
 unit to the left of
unit to the left of
 . Conversely,
. Conversely,
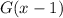 is
is
 unit to the right of
unit to the right of
 . The new function is to the left of
. The new function is to the left of
 . Meaning that
. Meaning that
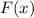 should should add
should should add
 to (rather than subtract
to (rather than subtract
 from) the independent variable of
from) the independent variable of
 . That rules out choice B) and D).
. That rules out choice B) and D).
- Multiplying a function by a number that is greater than one will stretch its graph vertically.
- Multiplying a function by a number that is between zero and one will compress its graph vertically.
- Multiplying a function by a number that is between
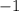 and zero will flip its graph about the
and zero will flip its graph about the
 -axis. Doing so will also compress the graph vertically.
-axis. Doing so will also compress the graph vertically. - Multiplying a function by a number that is less than
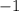 will flip its graph about the
will flip its graph about the
 -axis. Doing so will also stretch the graph vertically.
-axis. Doing so will also stretch the graph vertically.
The graph of
 is stretched vertically. However, similarly to the graph of this graph
is stretched vertically. However, similarly to the graph of this graph
 , the graph of
, the graph of
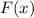 increases as
increases as
 increases. In other words, the graph of
increases. In other words, the graph of
 isn't flipped about the
isn't flipped about the
 -axis.
-axis.
 should have been multiplied by a number that is greater than one. That rules out choice C) and D).
should have been multiplied by a number that is greater than one. That rules out choice C) and D).
Overall, only choice A) meets the requirements.
Since the plot in the question also came with a couple of gridlines, see if the points
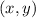 's that are on the graph of
's that are on the graph of
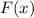 fit into the expression
fit into the expression
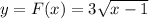 .
.