Your mouse pointer is covering the number at the hypotenuse, but I assume that it is 10.
We can test to see if the triangle is a right angled triangle by using Pythagoras' Theorem. This is because the Pythagorean Theorem only works with right angled triangles.
The theorem is:
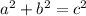
where:
a = length of one leg of the triangle
b = length of the other leg of the triangle
c = the length of the hypotenuse.
If triangle FGH is a right triangle then:
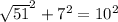
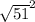 is just 51
is just 51
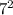 is 49
is 49
and
 is 100
is 100
if we add up 51 and 49 we get 100. And of course, 100 = 100,
Since the theorem works, then the FGH is a right triangle
______________________________________
Answer:
True: FGH is a right angled triangle