Question

A baseball is thrown into the air with an upward velocity of 30 ft/s. its initial height was 6 ft, and its maximum height is 20.06 ft. how long will it take the ball to reach its maximum height? round to the nearest hundredth.

i've been stuck on this question for almost an hour so if anyone can help that would be greatly appreciated

Answer 1

Explanation:

I'm not sure if this question is coming from a physics class or an algebra 2 or higher math class, but either way, the behavior of a parabola is the same in both subjects. If a parabola crosses the x axis, those 2 x values are called zeros of the polynomial. Those zeros translate to the time an object was initially launched and when it landed. The midpoint is dead center of where those x values are located. For example, if an object is launched at 0 seconds and lands on the ground 3 seconds later, it reached its max height at 2 seconds. So what we need to do is find the zeros of this particular quadratic, and the midpoint of those 2 values is where the object was at a max height of 20.06.

I used the physics equation representing parabolic motion for this, since it has an easier explanation. This equation is

`x-x_(0)=v_(0)+(1)/(2)at^2`

where x is the max height, x₀ is the initial height, v₀ is the initial upwards velocity, t is time (our unknown as of right now), and a is the acceleration due to gravity (here, -32 ft/sec^2). Filling in our values gives us this quadratic equation:

`20.06-6=30(t)+(1)/(2)(-32)t^2`

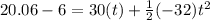
Simplifying that a bit gives us

`14.06=30t-16t^2`

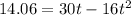
Rearranging into standard form looks like this:

`0=-16t^2+30t-14.06`

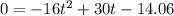
If we factor that using the quadratic formula we find that the 2 times where the ball was launched and then where it came back down are

t = .925 and .95 (the ball wasn't in the air for very long!)

The midpoint occurs between those 2 t values, so we find the midpoint of those 2 values by adding them and dividing the sum in half:

`(.925+.95)/(2)=.9375`

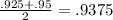
Therefore, the coordinates of the vertex (the max height) of this parabola are (.94, 20.06). That translates to: at a time of .94 seconds, the ball was at its max height of 20.06 feet

Answer 2

Check the picture below.

where is the -16t² coming from? that's Earth's gravity pull in feet.

`\bf ~~~~~~\textit{initial velocity} \\\\ \begin{array}{llll} ~~~~~~\textit{in feet} \\\\ h(t) = -16t^2+v_ot+h_o \end{array} \quad \begin{cases} v_o=\stackrel{30}{\textit{initial velocity of the object}}\\\\ h_o=\stackrel{6}{\textit{initial height of the object}}\\\\ h=\stackrel{}{\textit{height of the object at`

`\bf \textit{vertex of a vertical parabola, using coefficients} \\\\ h(t)=\stackrel{\stackrel{a}{\downarrow }}{-16}t^2\stackrel{\stackrel{b}{\downarrow }}{+30}t\stackrel{\stackrel{c}{\downarrow }}{+6} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right)`

`\bf \left(-\cfrac{30}{2(-16)}~~,~~6-\cfrac{30^2}{4(-16)} \right)\implies \left( \cfrac{30}{32}~,~6+\cfrac{225}{16} \right)\implies \left(\cfrac{15}{16}~,~\cfrac{321}{16} \right) \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill (\stackrel{\stackrel{\textit{how many}}{\textit{seconds it took}}}{0.9375}~~,~~\stackrel{\stackrel{\textit{how many feet}}{\textit{up it went}}}{20.0625})~\hfill`