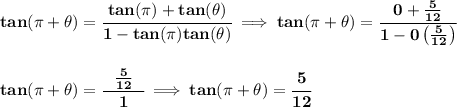Question

Find the value of tan( π + θ) if θ terminates in Quadrant III and sinθ = -5/13.

-5/13
-5/12
0
5/12

Answer 1

we know that θ is in the III Quadrant, and let's recall that on the III Quadrant sine and cosine are both negative, and since tangent = sine/cosine, that means that tangent is positive. Let's also keep in mind that tan(π) = sin(π)/cos(π) = 0/-1 = 0.

well, the hypotenuse is just a radius unit, so is never negative, since we know sin(θ) = -(5/13), well, the negative number must be the 5, so is really (-5)/13.

`\bf sin(\theta )=\cfrac{\stackrel{opposite}{-5}}{\stackrel{hypotenuse}{13}}\impliedby \textit{let's find the \underline{adjacent side}} \\\\\\ \textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2\implies \pm√(c^2-b^2)=a \qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(13^2-(-5)^2)=a\implies \pm√(144)=a\implies \pm 12 =a\implies \stackrel{III~Quadrant}{-12=a} \\\\[-0.35em] ~\dotfill`

`\bf tan(\theta )\implies \cfrac{sin(\theta )}{cos(\theta )}\implies \cfrac{~~-(5)/(13)~~}{-(12)/(13)}\implies -\cfrac{5}{~~\begin{matrix} 13 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}* -\cfrac{~~\begin{matrix} 13 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}{12}\implies \cfrac{5}{12} \\\\[-0.35em] ~\dotfill`

`\bf tan(\pi +\theta )=\cfrac{tan(\pi )+tan(\theta )}{1-tan(\pi )tan(\theta )}\implies tan(\pi +\theta )=\cfrac{0+(5)/(12)}{1-0\left( (5)/(12) \right)} \\\\\\ tan(\pi +\theta )=\cfrac{~~(5)/(12)~~}{1}\implies tan(\pi +\theta )=\cfrac{5}{12}`