Answer:
1. The probability that the student will get exactly 6 correct answers is
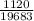 .
.
2. The probability that the student will get more than 6 correct answers is
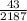 .
.
Explanation:
From the given information it is clear that
The total number of equations (n) = 10
The probability of selecting the correct answer (p)=

The probability of selecting the incorrect answer (q)=

According to the binomial distribution, the probability of selecting r items from n items is
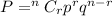
where, p is probability of success and q is the probability of failure.
The probability that the student will get exactly 6 correct answers is
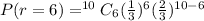
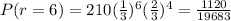
Therefore the probability that the student will get exactly 6 correct answers is
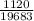 .
.
The probability that the student will get more than 6 correct answers is
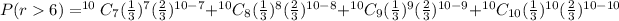
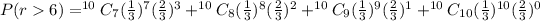
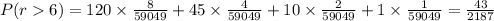
Therefore the probability that the student will get more than 6 correct answers is
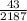 .
.