Question

A boat travels 33 miles downstream in 4 hours. The return trip takes the boat 7 hours. Find the speed of the boat in still water.

Answer 1

`6.48(mi)/(h)`

Explanation:

Let' call "b" the speed of the boat and "c" the speed of the river.

We know that:

`V=(d)/(t)`

Where "V" is the speed, "d" is the distance and "t" is the time.

Then:

`d=V*t`

We know that distance traveled downstream is 33 miles and the time is 4 hours. Then, we set up the folllowing equation:

`4(b+c)=33`

For the return trip:

`7(b-c)=33` (Remember that in the return trip the speed of the river is opposite to the boat)

By solving thr system of equations, we get:

- Make both equations equal to each other and solve for "c".

`4(b+c)=7(b-c)\\\\4b+4c=7b-7c\\\\4c+7c=7b-4b\\\\11c=3b\\\\c=(3b)/(11)`

- Substitute "c" into any original equation and solve for "b":

`4b+(3b)/(11) =33\\\\4b+(12b)/(11)=33\\\\(56b)/(11)=33\\\\b=6.48(mi)/(h)`

Answer 2

Speed of the boat in still water = 6.125 miles/hour

Explanation:

We are given that a boat travels 33 miles downstream in 4 hours and the return trip takes the boat 7 hours.

We are to find the speed of the boat in the still water.

Assuming
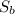`S_b` to be the speed of the boat in still water and
`S_w` to be the speed of the water.

The speeds of the boat add up when the boat and water travel in the same direction.

`Speed = (distance)/(time)`

`S_b+S_w=(d)/(t_1)=(33 miles)/(4 hours)`

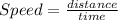
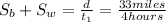
And the speed of the water is subtracted from the speed of the boat when the boat is moving upstream.

`S_b-S_w=(d)/(t_2)=(33 miles)/(7 hours)`

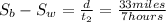
Adding the two equations to get:

`S_b+S_w=(d)/(t_1)`

+
`S_b-S_w=(d)/(t_2)`

___________________________

`2S_b=(d)/(t_1) +(d)/(t_2)`

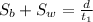
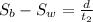
Solving this equation for
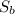`S_b` and substituting the given values for
`d,t_1, t_2`:

`S_b=((t_1+t_2)d)/(2t_1t_2)`

`S_b=((4 hour + 7hour)33 mi)/(2(4hour)(7hour))`

`S_b=((11 hour)(33mi))/(56hour^2)`

`S_b=6.125 mi/hr`

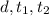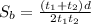
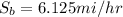
Therefore, the speed of the boat in still water is 6.125 miles/hour.