Answer:
The correct option is 2. The given function is a polynomial of degree 4 with a leading coefficient of 36.
Explanation:
A polynomial function is defined as
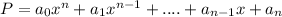
The given function is
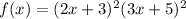
Using perfect square trinomial property.
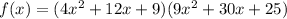
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/a4ffb4tvrpo42nxyev3p27dcpol4fcd030.png)
Using distributive property, we get
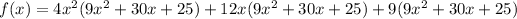

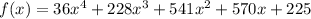
The given function is a polynomial of degree 4 with a leading coefficient of 36.
Therefore the correct option is 2.