Question

Write the equation of the line that is perpendicular to the line 5y=x−5 through the point (-1,0).

A. y= 1/5x+5
B. y= 1/5x−5
C. y= −5x−5
D. y= −5x+5

Answer 1

Steps:

---> Re arrange equation to get the format: y = mx + c

---> Work out the perpendicular gradient from the first equation

----> Substitute the x and y coordinates of point (-1, 0) and the perpendicular gradient into y = mx + c and work out c

---> Finally, substitute the perpendicular gradient and the value for c into y =mx + c to get the gradient of the perpendicular line:

__________________________________________

Rearranging equation into the format: y = mx + c:

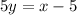`5y = x - 5` (Just divide both sides by y)

`y = (1)/(5)x -1`

___________________________________________

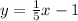
Working out the perpendicular gradient:

To work out the perpendicular gradient, we just take the negative reciprocal of the gradient of
`y = (1)/(5)x -1`

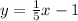
Note: negative reciprocal means we just flip the fraction and put a minus sign.

The regular gradient is:
`(1)/(5)`

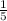
So the perpendicular gradient is the negative reciprocal of
`(1)/(5)`

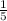
which is -5 (note:
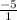`(-5)/(1)` is just 5-)

___________________________________________

Now lets substitute in the values for the gradient (m), the y coord (0) and x coord (-1) of the point (-1, 0) into y = mx + c, and solve for c:

y = mx + c (substitute in all known values)

0 = -5(-1) + c (the -1 times -5 will make + 5)

0 = 5 + c (subtract 5 from both sides to cancel out the + 5)

-5 = c

so c = -5

____________________________________________

Finally, just substitute in the perpendicular gradient and the value for c into y = mx + c to get the equation of the perpendicular line:

y = mx + c (substitute in the perp. gradient and c)

y = -5x - 5

____________________________________________________

Answer:

The equation to the line perpendicular to 5y = x - 5 through point (-1, 0) is :

C. y = -5x - 5

_______________________________________________

A quicker way to get equation of the perpendicular line once you know the perp. gradient is to use the equation:

y - y1 = m (x - x1)

y1 is the y coordinate of (-1, 0)

x1 is the x coordinate of (-1, 0)

m is the perpendicular gradient.

y - y1 = m (x - x1) (Substitute in values)

y - 0 = -5 ( x - - 1) (simplify)

y = -5 (x + 1) (expand the brackets)

y = -5x - 5