Question

Factor completely.

81x4-1
A. (3x + 1)(3x - 1)(3x + 1)(3x - 1)
B. 9x?(9x2 - 1)
C. (9x2 + 1)(9x2 - 1)
D. (9x2 + 1)(3x + 1)(3x - 1)
Reset
Next

Answer 1

Answer: Option D

`(9x^2+1)(3x+1)(3x-1)`

Explanation:

We have the following expression

`81x^4-1`

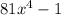
We can rewrite the expression in the following way:

`(9x^2)^2-1^2`

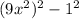
Remember the following property

`(a+b)(a-b) = a^2 -b^2`

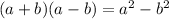
Then in this case
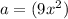`a=(9x^2)` and
`b=1`

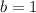
So we have that

`(9x^2)^2-1^2`

`(9x^2+1)(9x^2-1)`

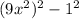
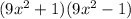
Now we can rewrite the expression
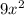`9x^2` as follows

`(3x)^2`

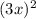
So

`(9x^2+1)(9x^2-1) =(9x^2+1)((3x)^2-1^2)`

Then in this case
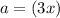`a=(3x)` and
`b=1`

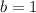
So we have that

`(9x^2+1)(9x^2-1) =(9x^2+1)((3x)^2-1^2)`

`(9x^2+1)(9x^2-1) =(9x^2+1)(3x+1)(3x-1)`

finally the factored expression is:

`(9x^2+1)(3x+1)(3x-1)`