Answer:

Explanation:
Note that we have a cudratic function of negative principal coefficient.
The minimum value reached by this function is found in its vertex.
For a quadratic function of the form

the x coordinate of the vertex is given by the following expression
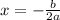
In this case the function is:
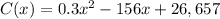
So:
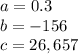
Then the x coordinate of the vertex is:
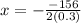

Then the number of machines that must be made to minimize the cost is:
