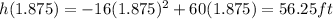Question

A ball is thrown vertically upward. After t seconds, its height h (in feet) is given by the function h(t) = 60t - 16t^2 . What is the maximum height that the ball will reach?

Do not round your answer.

Answer 1

56.25 feet.

Explanation:

h(t) = 60t - 16t^2

Differentiating to find the velocity:

v(t) = 60 -32t

This equals zero when the ball reaches its maximum height, so

60-32t = 0

t = 60/32 = 1.875 seconds

So the maximum height is h(1.875)

= 60* 1.875 - 16(1.875)^2

= 56.25 feet.

Answer 2

Answer: 56.25 feet.

Explanation:

For a Quadratic function in the form
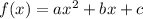`f(x)=ax^2+bx+c`, if
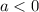`a<0` then the parabola opens downward.

Rewriting the given function as:

`h(t) = - 16t^2+60t`

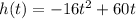
You can identify that
`a=-16`

Since
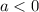`a<0` then the parabola opens downward.

Therefore, we need to find the vertex.

Find the x-coordinate of the vertex with this formula:

`x=(-b)/(2a)`

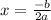
Substitute values:

`x=(-60)/(2(-16))=1.875`

Substitute the value of "t" into the function to find the height in feet that the ball will reach. Then:

`h(1.875)=- 16(1.875)^2+60(1.875)=56.25ft`