Answer:
The correct option is A. The given statement is true.
Explanation:
Given statement: If A and B are two points in the plane , the perpendicular bisector of AB is the set of all points equidistant from A and B.
Let a line is perpendicular bisector of AB at point D and C be a random point of perpendicular bisector.
In triangle ACD and BCD,
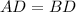 (Definition of perpendicular bisector)
(Definition of perpendicular bisector)
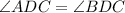 (Definition of perpendicular bisector)
(Definition of perpendicular bisector)
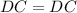 (Reflexive property)
(Reflexive property)
By SAS postulate of congruence,

The corresponding parts of congruent triangles are congruent.
 (CPCTC)
(CPCTC)

The distance between A to C and B to C are same. So, the set of all points on perpendicular bisector are equidistant from A and B.
The given statement is true. Therefore the correct option is A.