Answer:
The probability that we shall make exactly n selections is
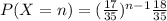 .
.
Explanation:
It is given that an urn contains 4 white and 4 black balls and we randomly choose 4 balls. If 2 of them are white and 2 are black, we stop.
The total number of ways to select exactly 2 white and 2 black balls.
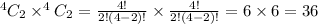
The total number of ways to select 4 balls from 8 balls is
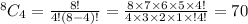
The probability of selecting exactly 2 white and 2 black balls is

The probability of not selecting exactly 2 white and 2 black balls is
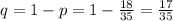
If we not get exactly 2 white and 2 black balls, then we replace the balls in the urn and again randomly select 4 balls.
The probability that we shall make exactly n selections is
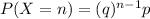
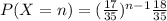
Therefore the probability that we shall make exactly n selections is
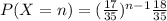 .
.