Answer with explanation:
Given :
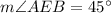
 is a right angle.
is a right angle.

To prove that : Bisect
 .
.
Proof: We are given that
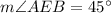

By definition of a right angle.
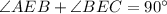
45+
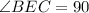
By substitution property
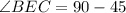
By subtraction property of equality

So,

Because they have the same measure.
Since BE divided the angle AEC into two congruent angles.Therefore, it is the angle bisector.
Hence proved.