Answer: 0.3446
Explanation:
Given : Mean :

Standard deviation :
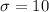
Also, the reading speed of second grade students in a large city is approximately normal.
Then , the formula to calculate the z-score is given by :_

For x = 94
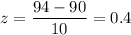
The p-value =
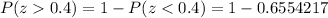
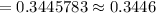
Hence, the probability a randomly selected student in the city will read more than 94 words per minute =0.3446