Answer:
1) 0.3456
2) 0.6544.
Explanation:
Let X represents the event of recognizing the brand,
Given,
The probability of recognizing the brand, p = 40% = 0.40,
Thus, the probability of not recognizing the brand, q = 1 - 0.40 = 0.60,
Since, the binomial distribution formula,
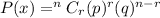
Where,
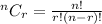
1) Thus, the probability that exactly 2 of the 5 consumers recognize the brand name is,
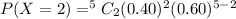
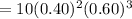
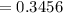
2) Also, the probability that the number who recognize the brand name is not 2 = 1 - P(X=2) = 1 - 0.3456 = 0.6544.