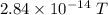Question

A proton moves with a speed of 3.60 106 m/s horizontally, at a right angle to a magnetic field. What magnetic field strength is required to just balance the weight of the proton and keep it moving horizontally? (The mass and charge of the proton are 1.67 ✕ 10−27 kg and 1.60 ✕ 10−19 C, respectively.) B = T

Answer 1

The magnetic field strength is required
`2.84*10^(-14)\ T`

Step-by-step explanation:

Given that,

Speed of proton
`v = 3.60*10^(6)\ m/s`

Mass of proton
`m_(p)=1.67*10^(-27)\ kg`

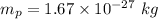
Charge
`q =1.60*10^(-19)\ C`

When a proton moves horizontally, at a right angle to a magnetic field .

Then, the gravitational force balances the magnetic field

`mg=Bqv\sin\theta`

`B = (mg)/(qv)`

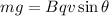
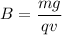
Here,
`\theta = 90^(\circ)`

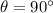
Where, B = magnetic field

q = charge

v = speed

Put the value into the formula

`B = (1.67*10^(-27)*9.8)/(1.60*10^(-19)*3.60*10^(6))`

`B = 2.84*10^(-14)\ T`

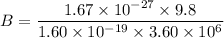
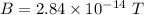
Hence, The magnetic field strength is required
`2.84*10^(-14)\ T`