Answer:
The acceleration of each of the two blocks and the tension in the rope are 5.92 m/s and 147.44 N.
Step-by-step explanation:
Given that,
Mass = 12.0 kg
Angle = 31.0°
Friction coefficient = 0.158
Mass of second block = 38.0 kg
Using formula of frictional force
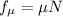 ....(I)
....(I)
Where, N = normal force

Put the value of N into the formula
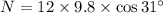
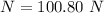
Put the value of N in equation (I)
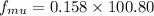
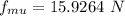
Now, Weight of second block
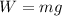
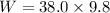
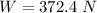
The horizontal force is
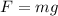
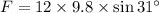
 ....(II)
....(II)
(I). We need to calculate the acceleration

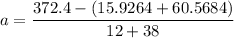
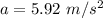
(II). We need to calculate the tension in the rope
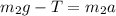
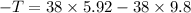

Hence, The acceleration of each of the two blocks and the tension in the rope are 5.92 m/s and 147.44 N.