Question

If ax7yb is a term from the expansion of (x + y)12, describe how to determine its coefficient a and missing exponent b without writing the entire expansion.

Answer 1

a) Use the homogeneous property of the binomial expansion to find the missing exponent

b) Use the binomial theorem to find the coefficient

Step-by-step explanation

The given binomial expansion is:

`(x+y)^(12)`

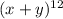
When we compare this to

`(a + b) ^(n)`

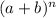
We have

`n = 12`

Therefore the of each term in the expansion must be 12.

`\implies \: 7 + b = 12`

`b = 12 - 7`

`b = 5`

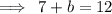
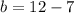
Since the coefficient of x and y are unity, we use the formula

`^(n) C_r = (n!)/((n - r)!r!)`

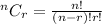
to find the coefficient.

Where n=12 and r=5(the exponent of the y-term).

Therefore the coefficient is

`^(12) C_5= (12!)/((12- 5)!5!)`

`^(12) C_5= (12!)/(7!5!)`

`^(12) C_5= (12 * 11 * 10 * 9 * 8 * 7!)/(7! * 5 * 4 * 3 * 2 * 1)`

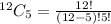
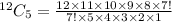
When we simplify further we get:

`^(12) C_5= 11 * 9 * 8 = 792`